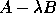We have written codes that solve one of the hardest problems of numerical linear algebra: spectral decomposition of nonsymmetric matrices. Our implementation uses only highly efficient matrix computation kernels, which are available in the public domain and from distributed memory parallel computer vendors. The performance attained is encouraging. This approach merits consideration for other numerical algorithms.
The object oriented user interface XI developed in this paper provides a paradigm for us in the future to design a more user friendly interface in the massively parallel computing environment.
We note that all the approaches discussed here can be extended to
compute the both right and left deflating subspaces of a regular
matrix pencil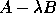 
. See [7][4] for
more details.
As the spectrum is repeatedly partitioned in a divide-and-conquer fashion, there is obviously task parallelism available because of the independent submatrices that arise, as well as the data parallel-like matrix operations considered in this paper. Analysis in [13] indicates that this task parallelism can contribute at most a small constant factor speedup, since most of the work is at the root of the divide-and-conquer tree. This can simplify the implementation.
Our future work will include the implementation and performance evaluation of the inverse free iteration based algorithm, comparison with parallel QR, the extension of the algorithms to the generalized spectral decomposition problem, and the integration of the 3-step approach (see section 2.3) to an object oriented user interface.