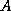 is distributed over a
is distributed over a  process grid with a block
cyclic distribution and a block size of
process grid with a block
cyclic distribution and a block size of 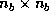 matching
the block size of the algorithm.
Thus, each
matching
the block size of the algorithm.
Thus, each 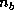 -wide column (or row) panel lies in one column (row)
of the process grid.
-wide column (or row) panel lies in one column (row)
of the process grid.
In this section, we first briefly describe the sequential, block-partitioned versions of the dense LU, QR, and Cholesky factorization routines of the LAPACK library. Since we also wish to discuss the parallel factorizations, we describe the right-looking versions of the routines. The right-looking variants minimize data communication and distribute the computation across all processes [17]. After describing the sequential factorizations, the parallel versions will be discussed.
For the implementation of the parallel block partitioned algorithms in
ScaLAPACK, we assume that a matrix 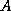 is distributed over a
is distributed over a  process grid with a block
cyclic distribution and a block size of
process grid with a block
cyclic distribution and a block size of 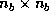 matching
the block size of the algorithm.
Thus, each
matching
the block size of the algorithm.
Thus, each 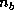 -wide column (or row) panel lies in one column (row)
of the process grid.
-wide column (or row) panel lies in one column (row)
of the process grid.
In the LU, QR and Cholesky factorization routines, in which the distribution of work becomes uneven as the computation progresses, a larger block size results in greater load imbalance, but reduces the frequency of communication between processes. There is, therefore, a tradeoff between load imbalance and communication startup cost which can be controlled by varying the block size.
In addition to the load imbalance that arises as distributed data are
eliminated from a computation, load imbalance may also arise due to
computational ``hot spots'' where certain processes have more work to
do between synchronization points than others.
This is the case, for example, in the LU factorization algorithm
where partial pivoting is performed over rows in a single column
of the process grid
while the other processes are idle.
Similarly, the evaluation of each block row of the  matrix requires
the solution of a lower triangular system across processes
in a single row of the process grid.
The effect of this type of load imbalance can be minimized through the choice
of
matrix requires
the solution of a lower triangular system across processes
in a single row of the process grid.
The effect of this type of load imbalance can be minimized through the choice
of  and
and  .
.