




Next: 6.2.5 Performance and Results
Up: Convectively-Dominated Flows and
Previous: 6.2.3 Parallel Issues
As a sample problem, the onset and growth of the Kelvin-Helmholtz
instability
was studied. This instability arises when the interface between two fluids
in shear motion is perturbed, and for this problem the body forces, 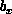 and
and
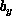 , are zero. In Figure 6.2 (Color Plate), we show the development of the
Kelvin-Helmholtz instability at the interface of two fluids in shear motion.
In these figures, the density of the massless marker particles normalized by
the fluid density is plotted on a color map, with red corresponding to a
density of one through green, blue, and white to a density of zero. Initially,
all the marker particles are in the upper half of the domain, and the fluids
in the lower- and upper-half domains have a relative shear velocity in the
horizontal direction. An
, are zero. In Figure 6.2 (Color Plate), we show the development of the
Kelvin-Helmholtz instability at the interface of two fluids in shear motion.
In these figures, the density of the massless marker particles normalized by
the fluid density is plotted on a color map, with red corresponding to a
density of one through green, blue, and white to a density of zero. Initially,
all the marker particles are in the upper half of the domain, and the fluids
in the lower- and upper-half domains have a relative shear velocity in the
horizontal direction. An 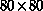 finite difference grid was used. Vortices form along the interface and
interact before being lost to numerical diffusion. By processing the
output from the nCUBE-1, a videotape of the evolution of the
instability was produced. This sample problem demonstrates that
the FCT technique is able to track the physical instability without
introducing numerical instability.
finite difference grid was used. Vortices form along the interface and
interact before being lost to numerical diffusion. By processing the
output from the nCUBE-1, a videotape of the evolution of the
instability was produced. This sample problem demonstrates that
the FCT technique is able to track the physical instability without
introducing numerical instability.
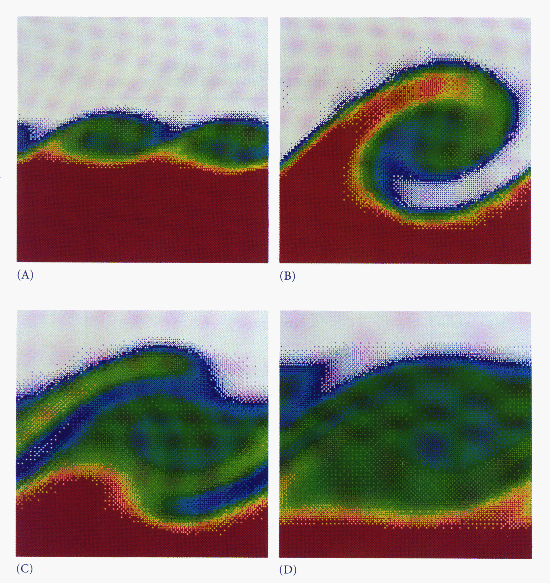
Figure 6.2: Development of the Kelvin-Helmholtz
instability at the interface of two fluids in shear motion.
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
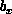 and
and
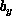 , are zero. In Figure 6.2 (Color Plate), we show the development of the
Kelvin-Helmholtz instability at the interface of two fluids in shear motion.
In these figures, the density of the massless marker particles normalized by
the fluid density is plotted on a color map, with red corresponding to a
density of one through green, blue, and white to a density of zero. Initially,
all the marker particles are in the upper half of the domain, and the fluids
in the lower- and upper-half domains have a relative shear velocity in the
horizontal direction. An
, are zero. In Figure 6.2 (Color Plate), we show the development of the
Kelvin-Helmholtz instability at the interface of two fluids in shear motion.
In these figures, the density of the massless marker particles normalized by
the fluid density is plotted on a color map, with red corresponding to a
density of one through green, blue, and white to a density of zero. Initially,
all the marker particles are in the upper half of the domain, and the fluids
in the lower- and upper-half domains have a relative shear velocity in the
horizontal direction. An 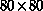 finite difference grid was used. Vortices form along the interface and
interact before being lost to numerical diffusion. By processing the
output from the nCUBE-1, a videotape of the evolution of the
instability was produced. This sample problem demonstrates that
the FCT technique is able to track the physical instability without
introducing numerical instability.
finite difference grid was used. Vortices form along the interface and
interact before being lost to numerical diffusion. By processing the
output from the nCUBE-1, a videotape of the evolution of the
instability was produced. This sample problem demonstrates that
the FCT technique is able to track the physical instability without
introducing numerical instability.





