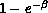The aim of the cluster update algorithms is to find a suitable collection of spins which can be flipped with relatively little cost in energy. We could obtain nonlocal updating very simply by using the standard Metropolis Monte Carlo algorithm to flip randomly selected bunches of spins, but then the acceptance would be tiny. Therefore, we need a method which picks sensible bunches or clusters of spins to be updated. The first such algorithm was proposed by Swendsen and Wang [Swendsen:87a], and was based on an equivalence between a Potts spin model [Potts:52a], [Wu:82a] and percolation models [Stauffer:78a], [Essam:80a], for which cluster properties play a fundamental role.
The Potts model is a very simple spin model of a
ferromagnet, in which the spins can take q different values. The
case q=2 is just the well-known Ising model. In the Swendsen and
Wang algorithm, clusters of spins are created by introducing bonds
between neighboring spins with probability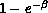 
if the two
spins are the same, and zero if they are not. All such clusters are
created and then updated by choosing a random new spin value for each
cluster and assigning it to all the spins in that cluster.
A variant of this algorithm, for which only a single cluster is constructed and updated at each sweep, has been proposed by Wolff [Wolff:89a]. The implementation of this algorithm is shown in Figures 12.23 through 12.25 (Color Plates), which show a q=3 Potts model at its critical temperature, with different colors representing the three different spin values. From the starting configuration (Figure 12.23 (Color Plate)), we choose a site at random, and construct a cluster around it by bonding together neighboring sites with the appropriate probabilities (Figure 12.24 (Color Plate)). All sites in this cluster are then given the same new spin value, producing the new configuration shown in Figure 12.25 (Color Plate), which is obviously far less correlated with the initial configuration than the result of a single Metropolis update (Figure 12.26 (Color Plate)). Although Wolff's method is probably the best sequential cluster algorithm, the Swendsen and Wang algorithm seems to be better suited for parallelization, since it involves the entire lattice rather than just a single cluster. We have, therefore, concentrated our attention on parallelizing the method of Swendsen and Wang, where all the clusters must be identified and labelled.
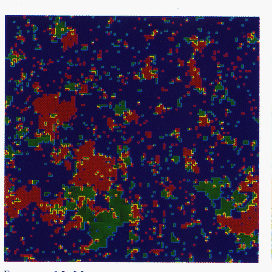
Figure 12_23: Initial configuration of 3-state Potts
spins on which Wolff Algorithm is to be applied.
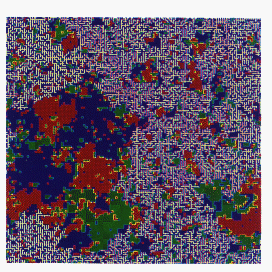
Figure 12_24: Configuration of figure 12.23 with bonds
of cluster constructed by Wolff Algorithm indicated in yellow.
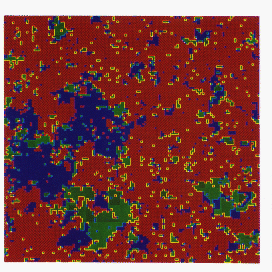
Figure 12_25: Results of Wolff Algorithm applied to
spin configuration in color Figure 12.23- all spins in cluster flipped to
same new value (in this case from blue to red).
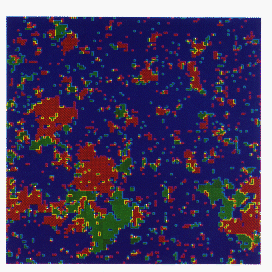
Figure 12_26: Results of Metropolis Algorithm applied
to spin configuration in Figure 12.23 - only a few single spins flipped.
First we outline a sequential method for labelling clusters, the so-called ``ants in the labyrinth'' algorithm. The reason for its name is that we can visualize the algorithm as follows [Dewar:87a]. An ant is put somewhere on the lattice, and notes which of the neighboring sites are connected to the site it is on. At the next time step, this ant places children on each of these connected sites which are not already occupied. The children then proceed to reproduce likewise until the entire cluster is populated. In order to label all the clusters, we start by giving every site a negative label, set the initial cluster label to be zero, and then loop through all the sites in turn. If a site's label is negative, then the site has not already been assigned to a cluster so we place an ant on this site, give it the current cluster label, and let it reproduce, passing the label on to all its offspring. When this cluster is identified, we increment the cluster label and carry on repeating the ant-colony birth, growth, and death cycle until all the clusters have been identified.