There is considerable current interest in performing accurate quantum mechanical, three-dimensional, reactive scattering cross section calculations. Accurate solutions have, until recently, proved to be difficult and computationally expensive to obtain, in large part due to the lack of sufficiently powerful computers. Prior to the advent of supercomputers, one could only solve the equations of motion for model systems or for sufficiently light atom-diatom systems at low energy [Schatz:75a;76a;76b]. As a result of the current development of efficient methodologies and increased access to supercomputers, there has been a remarkable surge of activity in this field. The use of symmetrized hyperspherical coordinates [Kuppermann:75a] and of the local hyperspherical surface function formalism [Hipes:87a], [Kuppermann:86a], [Ling:75a], has proven to be a successful approach to solving the three-dimensional Schrödinger equation [Cuccaro:89a;89b], [Hipes:87a], [Kuppermann:86a]. However, even for modest reactive scattering calculations, the memory and CPU demands are so great that even CRAY-type supercomputers will soon be insufficient to sustain progress.
In this section, we show how quantum mechanical reactive
scattering calculations can be structured so as to use MIMD-type
parallel computer architectures efficiently. We present a concurrent
algorithm for calculating local hyperspherical surface functions (LHSF)
and use a parallelized version [Hipes:88b] of Johnson's
logarithmic derivative method [Johnson:73a;77a;79a],
modified
to include the improvements suggested by Manolopoulos
[Manolopoulos:86a], for integrating the resulting coupled channel
reactive scattering equations. We compare the results of scattering
calculations on the Caltech/JPL Mark IIIfp 64-processor hypercube for
the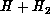 
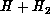system J=0,1,2 partial waves on the LSTH [Liu:73a],
[Siegbahn:78a], [Truhlar:78a;79a],
potential energy surface, with those of
calculations done on a CRAY X-MP/48 and a CRAY-2. Both accuracy and
performance are discussed, and speed estimates are made for the
Mark IIIfp 128-processor hypercube soon to become available and
compared with those of the San Diego Supercomputer Center CRAY Y-MP/864
machine which has recently been put into operation.