Poor Performance

ScaLAPACK ultimately relies on an efficient implementation of the BLAS  and the data distribution for load balance. Refer to Chapter 5.

To avoid poor performance  from ScaLAPACK routines, note the following recommendations :

BLAS:

One should use machine-specific optimized BLAS if they are available. Many manufacturers and research institutions have developed, or are developing, efficient versions of the BLAS for particular machines. The BLAS enable LAPACK and ScaLAPACK routines to achieve high performance with transportable software. Users are urged to determine whether such an implementation of the BLAS exists for their platform. When such an optimized implementation of the BLAS is available, it should be used to ensure optimal performance. If such a machine-specific implementation of the BLAS does not exist for a particular platform, one should consider installing a publicly available set of BLAS that requires only an efficient implementation of the matrix-matrix multiply BLAS routine xGEMM. Examples of such implementations are [35, 90]. A machine-specific and efficient implementation of the routine GEMM can be automatically generated by publicly available software such as [16]. Although a reference implementation of the Fortran77 BLAS is available from the blas directory on netlib, these routines are not expected to perform as well as a specially tuned implementation on most high-performance computers - on some machines it may give much worse performance - but it allows users to run LAPACK and ScaLAPACK software on machines that do not offer any other implementation of the BLAS.

BLACS:

With the few exceptions mentioned in section 5.2.3, the performance achieved by the BLACS should be close to the one of the underlying message-passing library it is calling. Since publicly available implementations of the BLACS exist for a range of native message-passing libraries such as NX for the Intel supercomputers and MPL for the IBM SP series, as well as more generic interfaces such as PVM and MPI, users should select the BLACS implementation that is based on the most efficient message-passing library available. Some vendors, such as Cray and IBM, supply an optimized implementation of the BLACS for their systems. Users are urged to rely on these BLACS libraries whenever possible.

LWORK 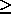WORK(1):

In some ScaLAPACK eigenvalue routines, such as the symmetric eigenproblems (PxSYEV and PxSYEVX/PxHEEVX) and the generalized symmetric eigenproblem (PxSYGVX/PxHEGVX), a larger value of LWORK can guarantee the orthogonality of the returned eigenvectors at the risk of potentially degraded performance of the algorithm. The minimum amount of workspace required is returned in the first element of the work array, but a larger amount of workspace can allow for additional orthogonalization if desired by the user. Refer to section 5.3.6 and the leading comments of the source code for complete details.