Release date: Fr 11/11/11.

This material is based upon work supported by the National Science Foundation and the Department of Energy under Grant No. NSF-OCI-1032861, NSF-CCF-00444486, NSF-CNS 0325873, NSF-EIA 0122599, NSF-ACI-0090127, DOE-DE-FC02-01ER25478, DOE-DE-FC02-06ER25768.

ScaLAPACK is a software package provided by Univ. of Tennessee, Univ. of California, Berkeley, and Univ. of Colorado Denver.

1. Support and questions

http://icl.cs.utk.edu/lapack-forum/

2. ScaLAPACK 2.0.0: What’s new

  1. PxHSEQR: Nonsymmetric Eigenvalue Problem. Contribution by Robert Granat, Bo Kågström, Meiyue Shao (Umeå University and HPC2N), and Daniel Kressner (École Polytechnique Fédérale de Lausanne). Compute the eigenvalues of a nonsymmetric real matrix. Implement the parallel distributed Hessenberg QR algorithm with the small bulge multi-shift QR algorithm together with aggressive early deflation. See reference [1] below.

  2. PxSYEVR/PxHEEVR: MRRR (Multiple Relatively Robust Representations) algorithm. Contribution by Christof Voemel. Compute the eigenvalues of a symmetric/Hermitian matrix. Implement the parallel distributed MRRR algorithm. See reference [2] below.

  3. BLACS revamping. Contribution by Rodney James (UC Denver).

3. References

[1]

Robert Granat, Bo Kågström, and Daniel Kressner. A Novel Parallel QR Algorithm for Hybrid Distributed Memory HPC Systems. SIAM J. Sci. Comput. 32(4):2345-2378, 2010.

[2]

Christof Voemel. ScaLAPACK’s MRRR Algorithm. ACM Transactions on Mathematical Software, 37(1):1-35, 2010.

4. External Contributors

  • Robert Granat, Umeå University and HPC2N

  • Bo Kågström, Umeå University and HPC2N

  • Daniel Kressner, École Polytechnique Fédérale de Lausanne

  • Meiyue Shao, Umeå University and HPC2N

  • Christof Voemel

5. Thanks

Thanks for bug-report/patches/suggestions to: Yana Gurieva (Intel MKL), dstrubbe, Jill Reese (MathWorks), François Thomas, Sebastian Tschiatschek and Joost VandeVondele.

6. Developer list

Principal Investigators

  • Jim Demmel (University of California, Berkeley, USA)

  • Jack Dongarra (University of Tennessee and ORNL, USA)

  • Julien Langou (University of Colorado Denver, USA)

LAPACK developers involved in this release

  • Rodney James (University of Colorado Denver, USA)

  • Julie Langou (University of Tennessee, USA)

7. More details

7.1. PxHSEQR: Nonsymmetric Eigenvalue Problem

contributors

Robert Granat, Umeå University and HPC2N, Bo Kågström, Umeå University and HPC2N, Daniel Kressner, École Polytechnique Fédérale de Lausanne, and Meiyue Shao, Umeå University and HPC2N

lapacker

Rodney James (UC Denver)

contribution

Compute the eigenvalues of a nonsymmetric real matrix. Implement the parallel distributed Hessenberg QR algorithm with the small bulge multi-shift QR algorithm together with aggressive early deflation.

  • PxHSEQR computes the eigenvalues of an upper Hessenberg matrix H and, optionally, the matrices T and Z from the Schur decomposition H = Z*T*ZT, where T is an upper quasi-triangular matrix (the Schur form), and Z is the orthogonal matrix of Schur vectors. Optionally Z may be postmultiplied into an input orthogonal matrix Q so that this routine can give the Schur factorization of a matrix A which has been reduced to the Hessenberg form H by the orthogonal matrix Q: A = Q*H*QT = (QZ)*T*(QZ)T.

  • PxGEBAL balances a general real matrix A. This involves, first, permuting A by a similarity transformation to isolate eigenvalues on the diagonal; and second, applying a diagonal similarity transformation to make the rows and columns as close in norm as possible. Both steps are optional. Balancing may reduce the 1-norm of the matrix, and improve the accuracy of the computed eigenvalues and/or eigenvectors.

reference

Robert Granat, Bo Kågström, and Daniel Kressner. A Novel Parallel QR Algorithm for Hybrid Distributed Memory HPC Systems. SIAM J. Sci. Comput. 32(4):2345-2378, 2010.

computational subroutines
pdhseqr.f       pshseqr.f
pdgebal.f       psgebal.f
      SUBROUTINE PDHSEQR( JOB, COMPZ, N, ILO, IHI, H, DESCH, WR, WI, Z,
     $                    DESCZ, WORK, LWORK, IWORK, LIWORK, INFO )
*
*     .. Scalar Arguments ..
      INTEGER            IHI, ILO, INFO, LWORK, LIWORK, N
      CHARACTER          COMPZ, JOB
*     ..
*     .. Array Arguments ..
      INTEGER            DESCH( * ) , DESCZ( * ), IWORK( * )
      DOUBLE PRECISION   H( * ), WI( N ), WORK( * ), WR( N ), Z( * )
      SUBROUTINE PDGEBAL( JOB, N, A, DESCA, ILO, IHI, SCALE, INFO )
*
      IMPLICIT NONE
*
*     .. Scalar Arguments ..
      CHARACTER          JOB
      INTEGER            IHI, ILO, INFO, N
*     ..
*     .. Array Arguments ..
      INTEGER            DESCA( * )
      DOUBLE PRECISION   A( * ), SCALE( * )
auxiliary subroutines
bdlaapp.f       bslaapp.f
bdlaexc.f       bslaexc.f
bdtrexc.f       bstrexc.f
dlaqr6.f        slaqr6.f
pbdtrord.f      pbstrord.f
pbdtrsen.f      pbstrsen.f
pdlaqr0.f       pslaqr0.f
pdlaqr1.f       pslaqr1.f
pdlaqr2.f       pslaqr2.f
pdlaqr3.f       pslaqr3.f
pdlaqr4.f       pslaqr4.f
pdlaqr5.f       pslaqr5.f
pdrot.f         psrot.f
pdhseqr.f       pshseqr.f
pdlamve.f       pslamve.f
pdgebal.f       psgebal.f
pilaenvx.f
piparmq.f
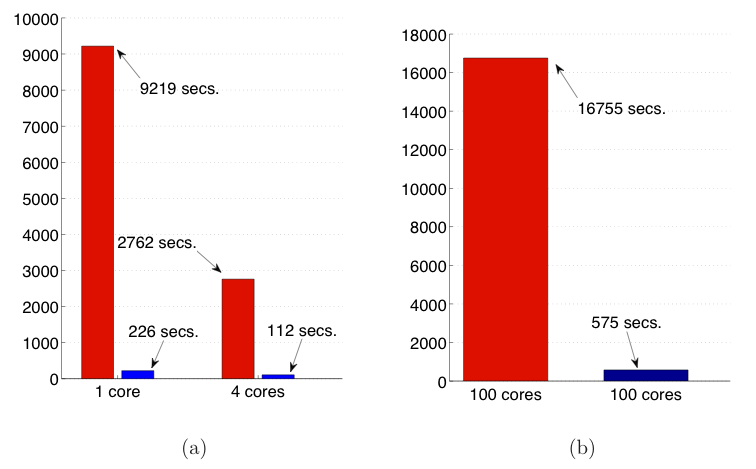
newpqr.png
Figure 1. Performance of previous ScaLAPACK implementation PDLAHQR (red left bars) vs. new implementation PDHSEQR (blue right bars)

The graph is extracted from reference [1] and the experiments have been performed by Robert Granat, Bo Kågström, and Daniel Kressner. This is using Intel Xeon quadcore nodes when computing the Schur form of a dense random matrix reduced to Hessenberg form. (a) Execution times for a 4000 x 4000 matrix using 1 or 4 cores of a single node. (b) Execution times for a 16 000 x 16 000 matrix using 100 cores of 25 nodes.

7.2. PxSYEVR/PxHEEVR: MRRR (Multiple Relatively Robust Representations) algorithm

contributors

Christof Voemel

lapacker

Rodney James (UC Denver)

contribution

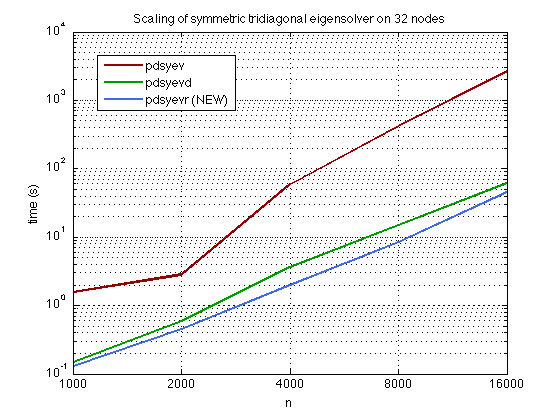
This parallel algorithm is derived from Parlett and Dhillon’s SIAG-LA prize-winning work on sequential MRRR. Compared to other algorithms, parallel MRRR has some striking advantages. First, for an n x n matrix on p processors, a tridiagonal inverse iteration can require up to O(n3) operations and O(n2) memory on a single processor to guarantee the correctness of the computed eigenpairs. MRRR is guaranteed to produce the right answer with O(n2/p) memory, and it does not need reorthogonalization. Second, MRRR allows the computation of subsets at reduced cost, whereas QR and Divide & Conquer do not. For computing k eigenpairs, the tridiagonal parallel MRRR requires O(nk/p) operations per processor.

reference

Christof Voemel. ScaLAPACK’s MRRR Algorithm. ACM Transactions on Mathematical Software, 37(1):1-35, 2010.

driver subroutines
pssyevr.f        pdsyevr.f        pcheevr.f        pzheevr.f
      SUBROUTINE PDSYEVR( JOBZ, RANGE, UPLO, N, A, IA, JA,
     $                    DESCA, VL, VU, IL, IU, M, NZ, W, Z, IZ,
     $                    JZ, DESCZ, WORK, LWORK, IWORK, LIWORK,
     $                    INFO )

*
*     .. Scalar Arguments ..
      CHARACTER          JOBZ, RANGE, UPLO
      INTEGER            IA, IL, INFO, IU, IZ, JA, JZ, LIWORK, LWORK, M,
     $                   N, NZ
      DOUBLE PRECISION VL, VU
*     ..
*     .. Array Arguments ..
      INTEGER            DESCA( * ), DESCZ( * ), IWORK( * )
      DOUBLE PRECISION   A( * ), W( * ), WORK( * ), Z( * )
auxiliary subroutines
slar1v.f         dlar1v.f
slar1va.f        dlar1va.f
slarra.f         dlarra.f
slarrb.f         dlarrb.f
slarrb2.f        dlarrb2.f
slarrc.f         dlarrc.f
slarrd.f         dlarrd.f
slarrd2.f        dlarrd2.f
slarre2.f        dlarre2.f
slarre2a.f       dlarre2a.f
slarrf.f         dlarrf.f
slarrf2.f        dlarrf2.f
slarrk.f         dlarrk.f
slarrv.f         dlarrv.f
slarrv2.f        dlarrv2.f
sstegr2.f        dstegr2.f
sstegr2a.f       dstegr2a.f
sstegr2b.f       dstegr2b.f
syev.png
Figure 2. Performance of ScaLAPACK implementation PDSYEV (red) and PDSYEVD (green) vs. the new PDSYEVR (blue)

7.3. BLACS revamping

lapacker

Rodney James (UC Denver)

contribution

With ScaLAPACK 2.0, the (MPI) BLACS is now completely integrated into ScaLAPACK. Linking a ScaLAPACK application now only requires linking with libscalapack.a, liblapack.a, libblas.a, and possibly the MPI libraries.