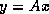 using CRS format can be
expressed in the usual way:
using CRS format can be
expressed in the usual way:
The matrix vector product 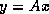 using CRS format can be
expressed in the usual way:
using CRS format can be
expressed in the usual way:

since this traverses the rows of the matrix  .
For an
.
For an 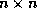 matrix A, the
matrix-vector multiplication is given by
matrix A, the
matrix-vector multiplication is given by
for i = 1, n
y(i) = 0
for j = row_ptr(i), row_ptr(i+1) - 1
y(i) = y(i) + val(j) * x(col_ind(j))
end;
end;
Since this method only multiplies nonzero matrix entries, the
operation count is 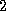 times the number of nonzero elements in
times the number of nonzero elements in  ,
which is a significant savings over the dense operation requirement
of
,
which is a significant savings over the dense operation requirement
of 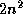 .
.
For the transpose product 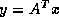 we cannot use the equation
we cannot use the equation
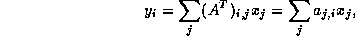
since this implies traversing columns of the matrix, an extremely inefficient operation for matrices stored in CRS format. Hence, we switch indices to
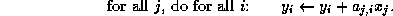
The matrix-vector multiplication involving 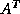 is then given by
is then given by
for i = 1, n
y(i) = 0
end;
for j = 1, n
for i = row_ptr(j), row_ptr(j+1)-1
y(col_ind(i)) = y(col_ind(i)) + val(i) * x(j)
end;
end;
Both matrix-vector products above have largely the same structure, and
both use indirect addressing. Hence, their vectorizability properties
are the same on any given computer. However, the first product
(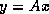 ) has a more favorable memory access pattern in that (per
iteration of the outer loop) it reads two vectors of data (a row of
matrix
) has a more favorable memory access pattern in that (per
iteration of the outer loop) it reads two vectors of data (a row of
matrix  and the input vector
and the input vector  ) and writes one scalar. The
transpose product (
) and writes one scalar. The
transpose product (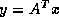 ) on the other hand reads one element of
the input vector, one row of matrix
) on the other hand reads one element of
the input vector, one row of matrix  , and both reads and writes the
result vector
, and both reads and writes the
result vector 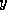 . Unless the machine on which these methods are
implemented has three separate memory paths (e.g., Cray Y-MP), the
memory traffic will then limit the performance. This is an
important consideration for RISC-based architectures.
. Unless the machine on which these methods are
implemented has three separate memory paths (e.g., Cray Y-MP), the
memory traffic will then limit the performance. This is an
important consideration for RISC-based architectures.