Block Compressed Row Storage (BCRS)





Next: Compressed Diagonal Storage
Up: Survey of Sparse
Previous: Compressed Column Storage
If the sparse matrix  is comprised of square
dense blocks of nonzeros in some regular pattern, we can modify
the CRS (or CCS) format to exploit such block patterns. Block
matrices typically arise from the discretization of partial differential
equations in which there are several degrees of freedom associated
with a grid point. We then partition the matrix in small blocks with
a size equal to the number of degrees of freedom, and treat each
block as a dense matrix, even though it may have some zeros.
is comprised of square
dense blocks of nonzeros in some regular pattern, we can modify
the CRS (or CCS) format to exploit such block patterns. Block
matrices typically arise from the discretization of partial differential
equations in which there are several degrees of freedom associated
with a grid point. We then partition the matrix in small blocks with
a size equal to the number of degrees of freedom, and treat each
block as a dense matrix, even though it may have some zeros.
If 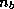 is the dimension of each block and
is the dimension of each block and 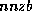 is the number of nonzero
blocks in the
is the number of nonzero
blocks in the 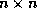 matrix
matrix  , then the total storage
needed is
, then the total storage
needed is 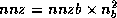 .
The block
dimension
.
The block
dimension 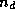 of
of  is then defined by
is then defined by 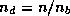 .
.
Similar to the CRS format, we require 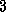 arrays for the BCRS format:
a rectangular array for floating-point numbers (
val(
arrays for the BCRS format:
a rectangular array for floating-point numbers (
val(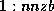 ,
, ,
, )) which stores the nonzero blocks in
(block) row-wise fashion, an integer array (col_ind(
)) which stores the nonzero blocks in
(block) row-wise fashion, an integer array (col_ind(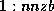 ))
which stores the actual column indices in the original matrix
))
which stores the actual column indices in the original matrix  of
the (
of
the (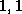 ) elements of the nonzero blocks, and a pointer
array (row_blk(
) elements of the nonzero blocks, and a pointer
array (row_blk( )) whose entries point to the beginning of
each block row in val(:,:,:) and col_ind(:). The
savings in storage locations and reduction in indirect addressing for
BCRS over CRS can be significant for matrices with a large
)) whose entries point to the beginning of
each block row in val(:,:,:) and col_ind(:). The
savings in storage locations and reduction in indirect addressing for
BCRS over CRS can be significant for matrices with a large 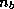 .
.
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
 is comprised of square
dense blocks of nonzeros in some regular pattern, we can modify
the CRS (or CCS) format to exploit such block patterns. Block
matrices typically arise from the discretization of partial differential
equations in which there are several degrees of freedom associated
with a grid point. We then partition the matrix in small blocks with
a size equal to the number of degrees of freedom, and treat each
block as a dense matrix, even though it may have some zeros.
is comprised of square
dense blocks of nonzeros in some regular pattern, we can modify
the CRS (or CCS) format to exploit such block patterns. Block
matrices typically arise from the discretization of partial differential
equations in which there are several degrees of freedom associated
with a grid point. We then partition the matrix in small blocks with
a size equal to the number of degrees of freedom, and treat each
block as a dense matrix, even though it may have some zeros.
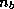 is the dimension of each block and
is the dimension of each block and 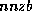 is the number of nonzero
blocks in the
is the number of nonzero
blocks in the 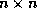 matrix
matrix 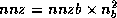 .
The block
dimension
.
The block
dimension 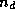 of
of 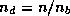 .
.
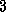 arrays for the BCRS format:
a rectangular array for floating-point numbers (
val(
arrays for the BCRS format:
a rectangular array for floating-point numbers (
val(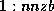 ,
, ,
,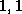 ) elements of the nonzero blocks, and a pointer
array (row_blk(
) elements of the nonzero blocks, and a pointer
array (row_blk( )) whose entries point to the beginning of
each block row in val(:,:,:) and col_ind(:). The
savings in storage locations and reduction in indirect addressing for
BCRS over CRS can be significant for matrices with a large
)) whose entries point to the beginning of
each block row in val(:,:,:) and col_ind(:). The
savings in storage locations and reduction in indirect addressing for
BCRS over CRS can be significant for matrices with a large