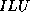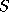 of matrix positions, and keeping all positions outside this
set equal to zero during the factorization. The resulting
factorization is incomplete in the sense that fill is suppressed.
of matrix positions, and keeping all positions outside this
set equal to zero during the factorization. The resulting
factorization is incomplete in the sense that fill is suppressed.
The most common type of incomplete factorization is based on taking a
set 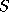 of matrix positions, and keeping all positions outside this
set equal to zero during the factorization. The resulting
factorization is incomplete in the sense that fill is suppressed.
of matrix positions, and keeping all positions outside this
set equal to zero during the factorization. The resulting
factorization is incomplete in the sense that fill is suppressed.
The set 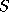 is usually chosen to encompass all positions
is usually chosen to encompass all positions 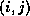 for
which
for
which 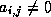 . A position that is zero in
. A position that is zero in  but not so in an
exact factorization
but not so in an
exact factorization![]() is called a fill position, and if it is
outside
is called a fill position, and if it is
outside 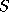 , the fill there is said to be ``discarded''.
Often,
, the fill there is said to be ``discarded''.
Often, 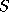 is chosen to coincide with the set of nonzero positions
in
is chosen to coincide with the set of nonzero positions
in  , discarding all fill. This factorization type is called
the
, discarding all fill. This factorization type is called
the 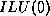 factorization: the Incomplete
factorization: the Incomplete 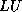 factorization of
level zero
factorization of
level zero![]() .
.
We can describe an incomplete factorization formally as
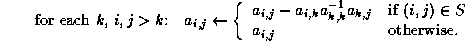
Meijerink and Van der Vorst [152] proved that, if  is
an
is
an 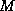 -matrix, such a factorization exists for any choice of
-matrix, such a factorization exists for any choice of 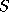 , and
gives a symmetric positive definite matrix if
, and
gives a symmetric positive definite matrix if  is symmetric
positive definite. Guidelines for allowing levels of fill were given
by Meijerink and Van der Vorst in [153].
is symmetric
positive definite. Guidelines for allowing levels of fill were given
by Meijerink and Van der Vorst in [153].
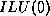 and
and 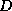 -
-