 of the linear system only via the
matrix-vector product
of the linear system only via the
matrix-vector product 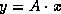 (and
perhaps
(and
perhaps 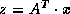 ). Thus the user need only supply a subroutine
for computing
). Thus the user need only supply a subroutine
for computing 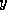 (and perhaps
(and perhaps  ) given
) given  , which permits full
exploitation of the sparsity or other special structure of
, which permits full
exploitation of the sparsity or other special structure of  .
.
Which of the following statements is true?
Traditionally, users have asked for and been provided with black box software in the form of mathematical libraries such as LAPACK , LINPACK , NAG , and IMSL . More recently, the high-performance community has discovered that they must write custom software for their problem. Their reasons include inadequate functionality of existing software libraries, data structures that are not natural or convenient for a particular problem, and overly general software that sacrifices too much performance when applied to a special case of interest.
Can we meet the needs of both groups of users? We believe we can. Accordingly, in this book, we introduce the use of templates Template: Description of an algorithm, abstracting away from implementational details. A template is a description of a general algorithm rather than the executable object code or the source code more commonly found in a conventional software library. Nevertheless, although templates are general descriptions of key algorithms, they offer whatever degree of customization the user may desire. For example, they can be configured for the specific data structure of a problem or for the specific computing system on which the problem is to run.
We focus on the use of iterative methods for solving large sparse systems of linear equations.Iterative method: An algorithm that produces a sequence of approximations to the solution of a linear system of equations; the length of the sequence is not given a priori by the size of the system. Usually, the longer one iterates, the closer one is able to get to the true solution. See: Direct method.Direct method: An algorithm that produces the solution to a system of linear equations in a number of operations that is determined a priori by the size of the system. In exact arithmetic, a direct method yields the true solution to the system. See: Iterative method.
Many methods exist for solving such problems. The trick is to find the most effective method for the problem at hand. Unfortunately, a method that works well for one problem type may not work as well for another. Indeed, it may not work at all.
Thus, besides providing templates, we suggest how to choose and
implement an effective method, and how to specialize a method to
specific matrix types. We restrict ourselves to iterative
methods, which work by repeatedly improving an approximate solution
until it is accurate enough. These methods access the coefficient
matrix  of the linear system only via the
matrix-vector product
of the linear system only via the
matrix-vector product 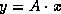 (and
perhaps
(and
perhaps 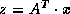 ). Thus the user need only supply a subroutine
for computing
). Thus the user need only supply a subroutine
for computing 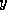 (and perhaps
(and perhaps  ) given
) given  , which permits full
exploitation of the sparsity or other special structure of
, which permits full
exploitation of the sparsity or other special structure of  .
.
We believe that after reading this book, applications developers will be able to use templates to get their program running on a parallel machine quickly. Nonspecialists will know how to choose and implement an approach to solve a particular problem. Specialists will be able to assemble and modify their codes-without having to make the huge investment that has, up to now, been required to tune large-scale applications for each particular machine. Finally, we hope that all users will gain a better understanding of the algorithms employed. While education has not been one of the traditional goals of mathematical software, we believe that our approach will go a long way in providing such a valuable service.