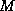 approximates the coefficient matrix
approximates the coefficient matrix  in some way, the transformed system
in some way, the transformed system
The convergence rate of iterative methods depends on spectral properties of the coefficient matrix. Hence one may attempt to transform the linear system into one that is equivalent in the sense that it has the same solution, but that has more favorable spectral properties. A preconditioner is a matrix that effects such a transformation.
For instance, if a matrix 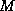 approximates the coefficient matrix
approximates the coefficient matrix  in some way, the transformed system
in some way, the transformed system

has the same solution as the original system  , but the spectral
properties of its coefficient matrix
, but the spectral
properties of its coefficient matrix 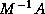 may be more favorable.
may be more favorable.
In devising a preconditioner, we are faced with a choice between finding
a matrix 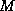 that approximates
that approximates  , and for which solving a system is
easier than solving one with
, and for which solving a system is
easier than solving one with  , or finding a matrix
, or finding a matrix 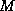 that
approximates
that
approximates 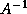 , so that only multiplication by
, so that only multiplication by 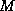 is needed.
The majority of preconditioners falls in the first category; a notable
example of the second category will be discussed in §
is needed.
The majority of preconditioners falls in the first category; a notable
example of the second category will be discussed in §![]() .
.