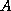 and the preconditioner
and the preconditioner 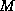 are both
symmetric) for the Chebyshev Iteration we have the same upper
bound as for the Conjugate Gradient
method, provided
are both
symmetric) for the Chebyshev Iteration we have the same upper
bound as for the Conjugate Gradient
method, provided  and
and  are computed from
are computed from 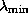 and
and  (the extremal eigenvalues of the preconditioned
matrix
(the extremal eigenvalues of the preconditioned
matrix 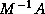 ).
).
In the symmetric case (where 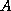 and the preconditioner
and the preconditioner 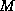 are both
symmetric) for the Chebyshev Iteration we have the same upper
bound as for the Conjugate Gradient
method, provided
are both
symmetric) for the Chebyshev Iteration we have the same upper
bound as for the Conjugate Gradient
method, provided  and
and  are computed from
are computed from 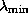 and
and  (the extremal eigenvalues of the preconditioned
matrix
(the extremal eigenvalues of the preconditioned
matrix 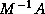 ).
).
There is a severe penalty for overestimating
or underestimating the field of values. For example, if in the
symmetric case  is underestimated, then the method may
diverge; if it is overestimated then the result may be very slow
convergence. Similar statements can be made for the nonsymmetric case.
This implies that one needs fairly accurate bounds on the
spectrum of
is underestimated, then the method may
diverge; if it is overestimated then the result may be very slow
convergence. Similar statements can be made for the nonsymmetric case.
This implies that one needs fairly accurate bounds on the
spectrum of 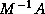 for the method to be effective (in comparison
with CG or GMRES).
for the method to be effective (in comparison
with CG or GMRES).