 (multiplied by a scalar) to vector
(multiplied by a scalar) to vector 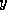
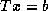 for triangular matrix
for triangular matrix 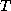
The BLAS give us a standardized set of basic codes for performing operations on vectors and matrices. BLAS take advantage of the Fortran storage structure and the structure of the mathematical system wherever possible. Additionally, many computers have the BLAS library optimized to their system. Here we use five routines:
 (multiplied by a scalar) to vector
(multiplied by a scalar) to vector 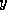
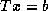 for triangular matrix
for triangular matrix 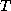
The prefix ``S'' denotes single precision. This prefix may be changed to ``D'', ``C'', or ``Z'', giving the routine double, complex, or double complex precision. (Of course, the declarations would also have to be changed.) It is important to note that putting double precision into single variables works, but single into double will cause errors.
If we define 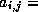 a(i,j) and
a(i,j) and 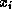 = x(i), we can see what the
code is doing:
= x(i), we can see what the
code is doing:
ALPHA = SDOT( N, X, 1, Y, 1 ) computes the inner product of two
vectors  and
and 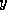 , putting the result in scalar
, putting the result in scalar  .
.
The corresponding Fortran segment is
ALPHA = 0.0 DO I = 1, N ALPHA = ALPHA + X(I)*Y(I) ENDDO
CALL SAXPY( N, ALPHA, X, 1, Y ) multiplies a
vector  of length
of length  by the scalar
by the scalar  , then adds the result to
the vector
, then adds the result to
the vector 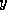 , putting the result in
, putting the result in 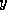 .
.
The corresponding Fortran segment is
DO I = 1, N Y(I) = ALPHA*X(I) + Y(I) ENDDO
CALL SGEMV( 'N', M, N, ONE, A, LDA, X, 1, ONE, B, 1 )
computes the matrix-vector product plus vector 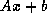 ,
putting the resulting vector in
,
putting the resulting vector in 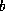 .
.
The corresponding Fortran segment:
DO J = 1, N
DO I = 1, M
B(I) = A(I,J)*X(J) + B(I)
ENDDO
ENDDO
This illustrates a feature of the BLAS that often requires close
attention. For example, we will use this routine to compute the residual
vector 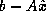 , where
, where  is our current approximation to the
solution
is our current approximation to the
solution  (merely change the fourth argument to -1.0E0). Vector
(merely change the fourth argument to -1.0E0). Vector 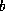 will be overwritten with the residual vector; thus, if we need it later, we
will first copy it to temporary storage.
will be overwritten with the residual vector; thus, if we need it later, we
will first copy it to temporary storage.
CALL STRMV( 'U', 'N', 'N', N, A, LDA, X, 1 ) computes the
matrix-vector product 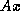 , putting the resulting vector in
, putting the resulting vector in  ,
for upper triangular matrix
,
for upper triangular matrix  .
.
The corresponding Fortran segment is
DO J = 1, N
TEMP = X(J)
DO I = 1, J
X(I) = X(I) + TEMP*A(I,J)
ENDDO
ENDDO
Note that the parameters in single quotes are for descriptions
such as 'U' for `UPPER TRIANGULAR', 'N' for `No Transpose'. This
feature will be used extensively, resulting in storage savings
(among other advantages).
The variable LDA is critical for addressing the array
correctly. LDA is the leading dimension of the two-dimensional
array A,
that is, LDA is the declared (or allocated) number
of rows of the two-dimensional array  .
.