 -step Iterative Methods
-step Iterative Methods
 -step Iterative Methods
-step Iterative MethodsThe methods discussed so far are all subspace methods, that is, in every iteration they extend the dimension of the subspace generated. In fact, they generate an orthogonal basis for this subspace, by orthogonalizing the newly generated vector with respect to the previous basis vectors.
However, in the case of nonsymmetric coefficient matrices the newly generated vector may be almost linearly dependent on the existing basis. To prevent break-down or severe numerical error in such instances, methods have been proposed that perform a look-ahead step (see Freund, Gutknecht and Nachtigal [101], Parlett, Taylor and Liu [172], and Freund and Nachtigal [102]).
Several new, unorthogonalized, basis vectors are generated and are then orthogonalized with respect to the subspace already generated. Instead of generating a basis, such a method generates a series of low-dimensional orthogonal subspaces.
The  -step iterative methods of Chronopoulos and
Gear [55] use this strategy of generating
unorthogonalized vectors and processing them as a block to reduce
computational overhead and improve processor cache behavior.
-step iterative methods of Chronopoulos and
Gear [55] use this strategy of generating
unorthogonalized vectors and processing them as a block to reduce
computational overhead and improve processor cache behavior.
If conjugate gradient methods are considered to generate a factorization of a tridiagonal reduction of the original matrix, then look-ahead methods generate a block factorization of a block tridiagonal reduction of the matrix.
A block tridiagonal reduction is also effected by the
Block Lanczos algorithm and the Block Conjugate Gradient
method (see O'Leary [163]).
Such methods operate on multiple linear systems with the same
coefficient matrix simultaneously, for instance with multiple right hand
sides, or the same right hand side but with different initial guesses.
Since these block methods use multiple search directions in each step,
their convergence behavior is better than for ordinary methods. In fact,
one can show that the spectrum of the matrix is effectively
reduced by the 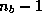 smallest eigenvalues, where
smallest eigenvalues, where 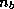 is the block
size.
is the block
size.