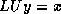CRS-based Factorization Solve

The system 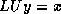can be solved in the usual manner by introducing a temporary vector :

We have a choice between several equivalent ways of solving the system:

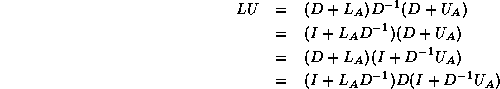
The first and fourth formulae are not suitable since they require both multiplication and division with 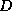; the difference between the second and third is only one of ease of coding. In this section we use the third formula; in the next section we will use the second for the transpose system solution.

Both halves of the solution have largely the same structure as the matrix vector multiplication.

for i = 1, n
    sum =  0
    for j = row_ptr(i), diag_ptr(i)-1
        sum = sum + val(j) * z(col_ind(j))
    end;
    z(i) = pivots(i) * (x(i)-sum)
end;   
for i = n, 1, (step -1)
    sum = 0
    for j = diag(i)+1, row_ptr(i+1)-1
        sum = sum + val(j) * y(col_ind(j))
        y(i) = z(i) - pivots(i) * sum
    end;
end;